Ligne de courant

Une ligne de courant est une courbe de l'espace décrivant le mouvement d'un fluide et qui, à tout instant, possède en tout point une tangente parallèle à la vitesse des particules du fluide.

Un tube de courant est un ensemble de lignes de courant s'appuyant sur un contour fermé (voir plus bas).

Lignes de courant dans un écoulement stationnaire

Cas simple de la plaque carrée exposée frontalement

Lorsque l'écoulement est stationnaire (que les vitesses locales ne varient ni en intensité ni en direction), on dit aussi écoulement permanent, le mouvement d'une poussière (de masse volumique égale à celle du fluide) emportée par cet écoulement trace une ligne de courant. Dans ce cas, les lignes de courant sont confondues avec les trajectoires et lignes d'émission.

Dans l'image ci-contre à gauche, la direction locale moyenne de la vitesse de l'air a été relevée avec « un fil court et très léger, porté à l'extrémité d'une tige mince, [en repérant] aussi exactement que possible la position et la direction du fil ». Dans les deux régions comprises entre les traits pointillés, les remous sont tels qu'on ne peut fixer une direction moyenne (on est donc en instationnaire).
Dans la pratique, il est assez fréquent qu'on moyenne les écoulements instationnaires et qu'on les traite à la façon des écoulements stationnaires. Ainsi la dépression qui se crée au culot d'une telle plaque carrée est-elle variable dans le temps et quand on donne un coefficient de traînée $C_{x}$ pour cette plaque carrée (ou même un coefficient de pression de culot), il s'agit toujours d'une moyenne temporelle.

Cas d'un profil en incidence

Faibles incidences

L'image ci-contre à gauche dessine par des séries de points les lignes de courant autour d'un profil à faible incidence. L'écoulement est stationnaire, c.-à-d. que les lignes de courant ne varient pas dans le temps. Comme on peut en juger, cependant, la vitesse d'une particule est fondamentalement variable sur sa ligne de courant : À l'extrados (au-dessus du profil), les particules sont globalement accélérées (cela commence même en avant du profil) ; à l'intrados (en dessous du profil), les particules sont globalement ralenties. En application du théorème de Bernoulli il se développe donc une dépression à l'extrados et une surpression à l'intrados. L'intégration des pressions locales sur l'extrados et l'intrados donnera donc une portance.
Si l'on préfère, on peut également observer que le profil imprime à l'ensemble des particules une composante de vitesse vers le bas : par usage de la troisième loi de Newton (loi action — réaction), on peut en tirer la conclusion que le profil est l'objet d'un portance. C'est ce qui fait dire parfois que les avions volent (se sustentent dans l'air) par réaction.

Fortes incidences

Lorsque l'incidence est trop forte, le profil est victime du phénomène de décrochage (image de droite). Cette captation en soufflerie montre bien la zone tourbillonnaire derrière le profil.

Définition mathématique de la ligne de courant

Considérons à titre d'exemple un fluide s'écoulant dans un tuyau. Plaçons-nous à un instant $t$ fixé dans le temps. En chaque point ${\vec {M}}(x_{1},x_{2},x_{3})$ du tube, l'écoulement a une certaine orientation indiquée par la direction de son vecteur vitesse ${\vec {V}}(x_{1},x_{2},x_{3},t)$ , de coordonnées $V_{1}(x_{1},x_{2},x_{3},t)$ , $V_{2}(x_{1},x_{2},x_{3},t)$ et $V_{3}(x_{1},x_{2},x_{3},t)$ (il s'agit d'une notion de l'approche eulérienne). Une ligne de courant à un instant $t$ est la ligne en tout point tangente au vecteur ${\vec {V}}(x_{1},x_{2},x_{3},t)$ (vecteur courant).

En considérant un petit élément ${\overrightarrow {dx}}$ parallèle à la ligne de courant, on doit avoir que le produit vectoriel ${\overrightarrow {dx}}\wedge {\overrightarrow {V}}={\overrightarrow {0}}$ car les deux vecteurs sont parallèles. Ainsi, en exprimant cette égalité, on obtient :

{\frac {\mathrm {d} x_{1}}{V_{1}}}={\frac {\mathrm {d} x_{2}}{V_{2}}}={\frac {\mathrm {d} x_{3}}{V_{3}}}

Les lignes de courant sont données en résolvant cette équation différentielle.

Une surface de courant est formée d'un ensemble de lignes de courant adjacentes ; aucune particule ne peut traverser une surface de courant.

Comparaison avec la trajectoire

Il convient généralement de distinguer la ligne de courant de la trajectoire d'une particule. L'une et l'autre ne sont confondues que dans le cas d'un écoulement stationnaire, c’est-à-dire un écoulement où ${\vec {V}}(x_{1},x_{2},x_{3})$ n'est pas fonction du temps $t$ (c.-à-d. que ${\frac {\partial {\vec {V}}}{\partial t}}={\vec {0}}$ , voir dérivée partielle). Dans le cas d'un écoulement instationnaire, les lignes de courant évoluent au cours du temps, alors que les trajectoires n'en dépendent intrinsèquement pas.

Tube de courant

On appelle tube de courant toute surface formée de lignes de courant s'appuyant sur un contour fermé. Par définition, la vitesse normale à la frontière est nulle et il n'y a donc pas de flux traversant les parois latérales ce tube, ce qui justifie que les particules y soient confinées, même si la forme des tubes de courant évolue généralement au cours du temps. En écoulement permanent, le débit entrant dans le tube de courant égale le débit sortant.

Visualisation des lignes de courant

Dans la nature, les plantes aquatiques donnent de bonnes indications sur la direction locale de l'eau dans un courant (image de gauche) ; cependant, quand ces plantes aquatiques sont longues, elles moyennent d'elles-mêmes les différents vecteurs vitesses de l'eau qui les porte et s'éloignent donc des véritables lignes de courant.
La présence de poussières dans un mouvement d'air permet souvent d'imaginer assez bien les lignes de courant dans ce mouvement (animation de droite).

Lorsqu'un écoulement d'air est stationnaire, une photographie en pause peut capter le mouvement de poussières ou, mieux, de bulles de savon gonflée à l'hélium (voir ci-dessous l'image du tourbillon marginal sur un Cessna), du moins si ces objets sont convenablement éclairés. Si l'écoulement, toujours stationnaire, est un écoulement d'eau, on peut placer dans cet écoulement des paillettes de matériaux brillants dont les reflets pourront être captés par photographie ou vidéo^,.

Mais la méthode la plus utilisée est d'émettre dans l'écoulement des filets de fumée comme dans les images ci-dessus à droite et ci-dessous. Dans les tests aérodynamiques d'automobiles, une lance à fumée unique permet d'étudier l'écoulement en rendant visible une unique ligne de courant ; l'observation de ce filet de fumée permet en particulier de vérifier que l'écoulement ne décolle pas à l'arrière du véhicule (image de droite, ci-dessous).

Utilité des lignes de courant

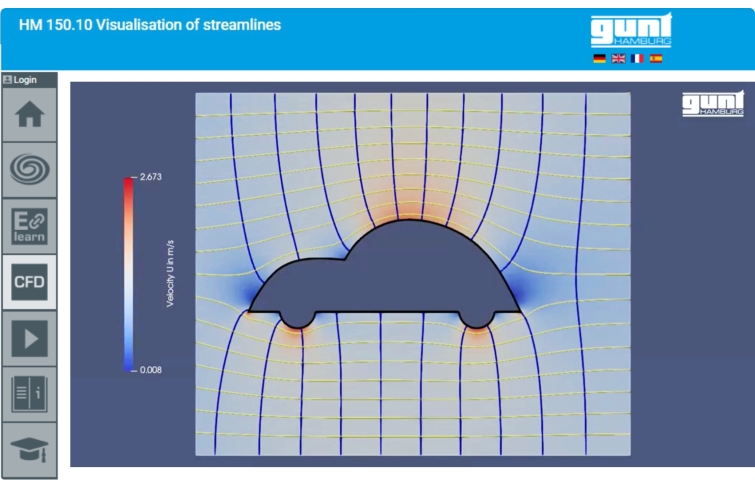
La première utilité des lignes de courant est pédagogique : dans un écoulement incompressible, lorsque l'écartement des lignes de courant diminue, la conservation des débits impose que la vitesse locale des particules est augmentée (donc que la pression statique de ces particules est diminuée, en application de la loi de Bernoulli) : près du maître couple d'un corps assez bien profilé (comme une voiture), il y a bien une survitesse (de quelque %) et, conséquemment, une dépression.
D'autre part, la connaissance des lignes de courant permet souvent d'isoler, dans un écoulement, les zones où se développent les tourbillons (comme dans les deux images ci-contre à gauche).

De même, la position des lignes de courant est révélatrice du régime de certain corps, comme la sphère (ci-contre à droite). Le même phénomène de régime existe pour le cylindre et beaucoup de corps profilés (voir l'article Crise de traînée).

Dans un écoulement stationnaire de fluide parfait (c.-à-d. non visqueux, donc en dehors de la couche limite), l’étude de l’équilibre des particules de fluides permet de démontrer que lorsqu’une ligne de courant est rectiligne la pression au long de cette ligne de courant est constante.
Inversement, toujours dans un écoulement stationnaire de fluide parfait, la même étude de l'équilibre des particules fluides permet de démontrer que la pression statique locale décroît lorsque l’on passe d’une ligne de courant à une autre en s’approchant du centre de courbure de ces lignes de courant.
On peut mettre en application ce dernier principe physique, par exemple dans l’image montrant ci-dessous les lignes de courant potentielles autour du cylindre : Lorsque l’on descend du milieu de l’image vers le cylindre, on se rapproche du centre de courbure des lignes de courant : la pression statique locale décroît donc (jusqu’au coefficient de pression $C_{p}=-3$ à l’épaule du cylindre, comme indiqué sur l'image). Par contre, lorsque l’on part du coin gauche en haut de la photo vers le point d’arrêt amont, on s’éloigne du centre de courbure des lignes de courant, la pression augmente donc (d’un $C_{p}$ presque nul, car on est loin du corps, jusqu’au $C_{p}$ unitaire au point d’arrêt). Même chose lorsque l’on part du coin droit de l’image et que l’on s’approche du point d’arrêt aval : la pression augmente jusqu’au $C_{p}$ unitaire.
D’une façon générale, ce principe vaut également pour les tourbillons d’échelle suffisante mais inférieure à l’échelle météorologique : la pression statique décroît lorsque l’on s’approche de l’axe du tourbillon ; c'est-à-dire qu’au cœur d’un tourbillon règne toujours une dépression (sauf à l’échelle météorologique).

D'autre part, en écoulement stationnaire incompressible, lorsque l'on connaît la vitesse moyenne dans une section donnée d'un tube de courant, la loi de conservation des débits impose une relation simple entre la section locale de ce tube de courant et la vitesse moyenne locale. L'image ci-dessous d'une contraction 2D montre une application de ce principe : La distribution des vitesses avant la contraction étant connue, la distribution des vitesses moyennes dans n'importe quelle autre section peut être calculée d'après l'espacement des lignes de courant au moyen de la formule : $V_{i}=V_{0}{\frac {\Delta h_{0}}{\Delta h_{i}}}$ , formule où $V_{0}$ est la vitesse moyenne connue dans la section d'indice $0$ d'un tube de courant et $i$ est l'indice attaché à la section considérée. Ci-dessous (troisième image) les lignes de courant autour d'un cylindre en rotation ont été matérialisées par de petites particules brillantes (cette image illustre un effet Magnus établi ; le fluide -de l'eau- circule de gauche à droite). En haut à gauche de l'image, deux lignes de courant ont été soulignées en rouge, ce qui forme un tube de courant (l’écoulement est bidimensionnel). La constance du débit dans le tube de courant ainsi défini veut que la vitesse augmente beaucoup entre la section d'entrée bleu clair de gauche et la section de sortie bleu clair de droite. En application du théorème de Bernoulli la pression est donc beaucoup plus faible dans le deuxième section que dans la première (on est en dehors de la couche limite existant autour du cylindre). C'est ce qui explique la création de la force de Magnus : une force vers le haut...

Lignes d'émission dans un écoulement instationnaire

Dans un écoulement instationnaire, le vecteur vitesse en un point fixe (par rapport au corps) varie au cours du temps. La ligne de courant ne peut donc plus être confondue avec la trajectoire des particules. C'est le cas dans l'image ci-contre. La ligne d'émission est la ligne que dessine à un instant t un filet de fumée ou de colorant émis dans le courant depuis un point fixe (l'origine des axes, ici). On peut donc facilement capter cette ligne d'émission par photographie. Lorsque l'écoulement est stationnaire, par contre, une ligne d'émission redevient une ligne de courant ainsi qu'une trajectoire de particule.

Notes et références

Bibliographie

(en) Johanna Vogel-Prandtl, Ludwig PANDTL, A PERSONAL BIOGRAPHY DRAWN FROM MEMORIES AND CORRESPONDENCE, Universitätsverlag Göttingen, 2014 (lire en ligne [PDF])